こんにちは、けーてんにゃです!今回はRの墨出しに関して解説していきます。
Rとは何か
まず始めに、Rとは何なのか?
一言で言うと半径・Radius (レェイディアス)の頭文字をとってR(アール)と呼びます。
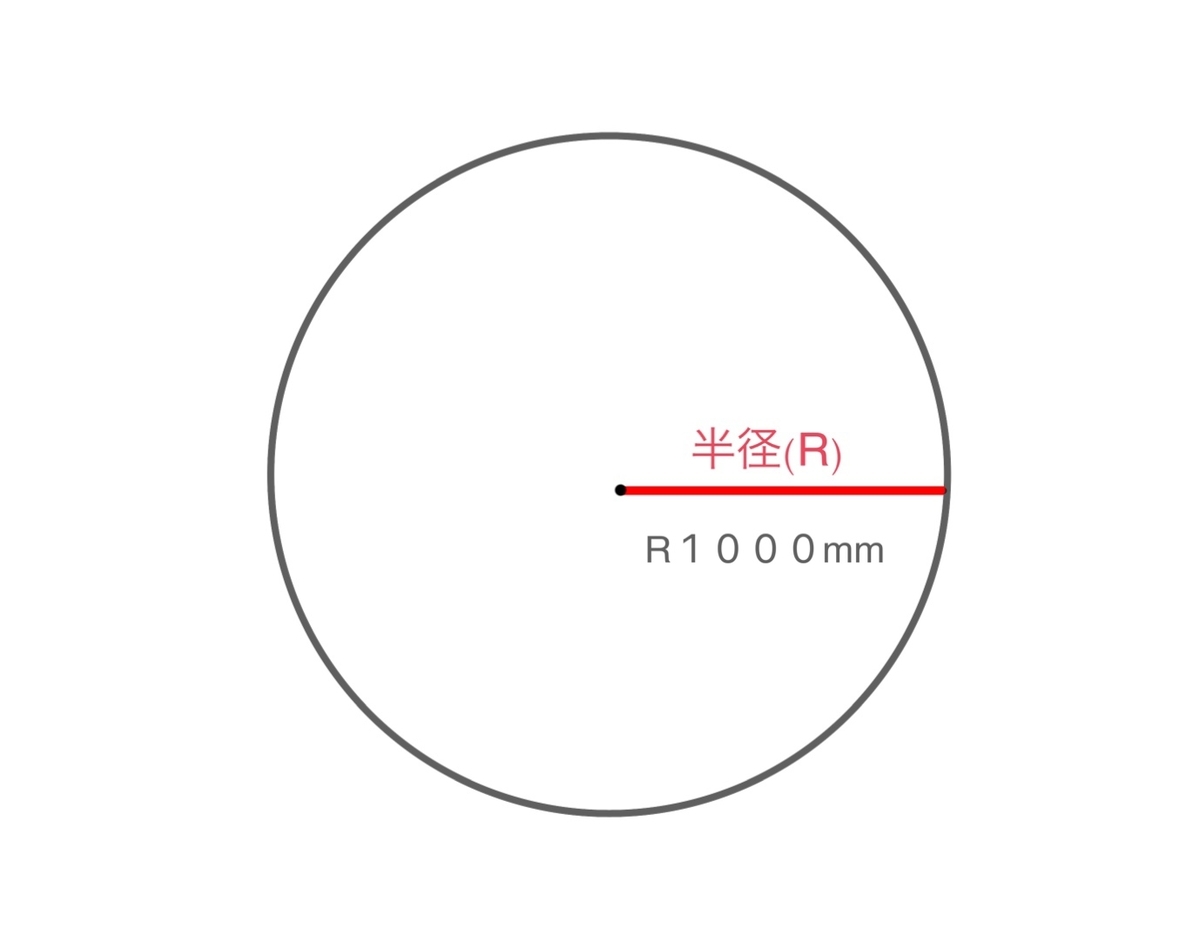
R 1000mmの円なら上図のように表され、曲面の壁などはR壁、曲面の部分や物のことをRの〜と言います。
図でRを理解する
単なる円にボードの厚みとLGSの厚み分も描き加えると下図のようになります。(エフジーボード6mm3枚と65型スタッドを使用した場合)
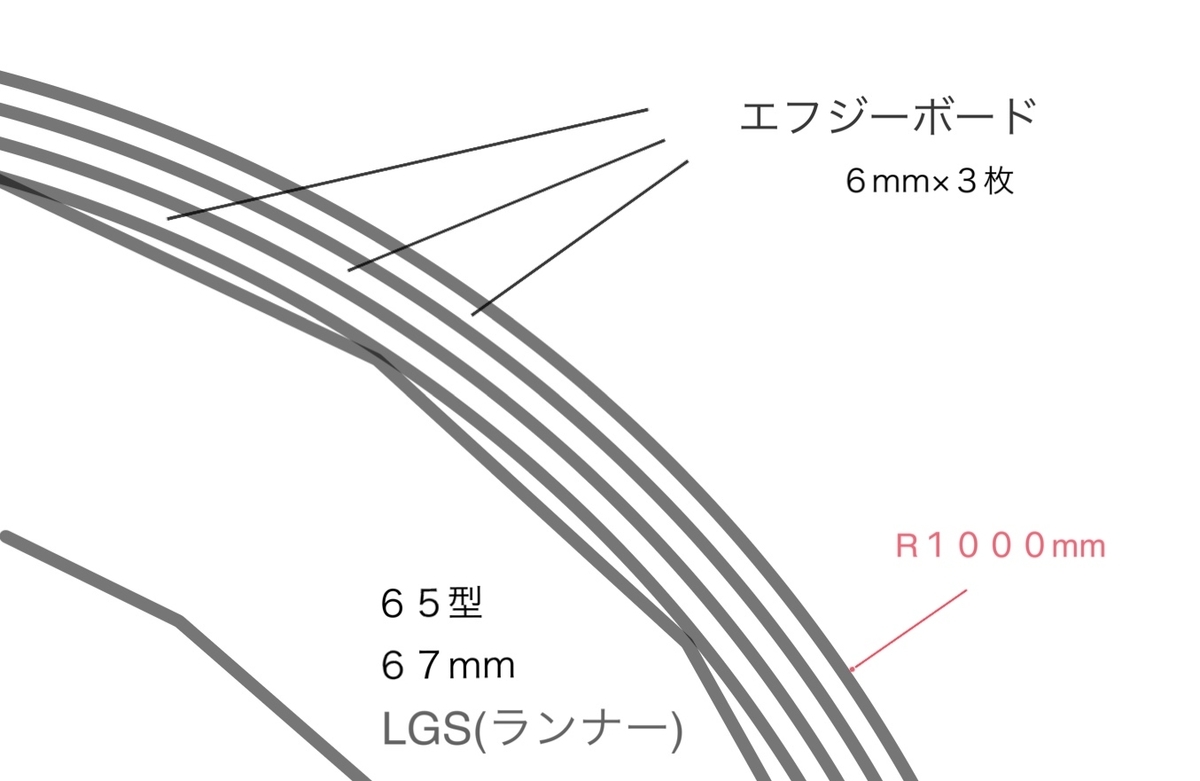
これだけを見るとRが簡単に思えてきたと思いますが、実際にRの墨出しを行うとなると面倒なことになっていきます。
簡単なRの墨出し
Rの壁の形を理解したところで、墨の出し方について考えていきます。
例えば 仕上がりの位置で R 1000mm 程度の小さなRの場合は、エフジーボード6mmを3枚貼る場合とすると、1000-18=982となります。
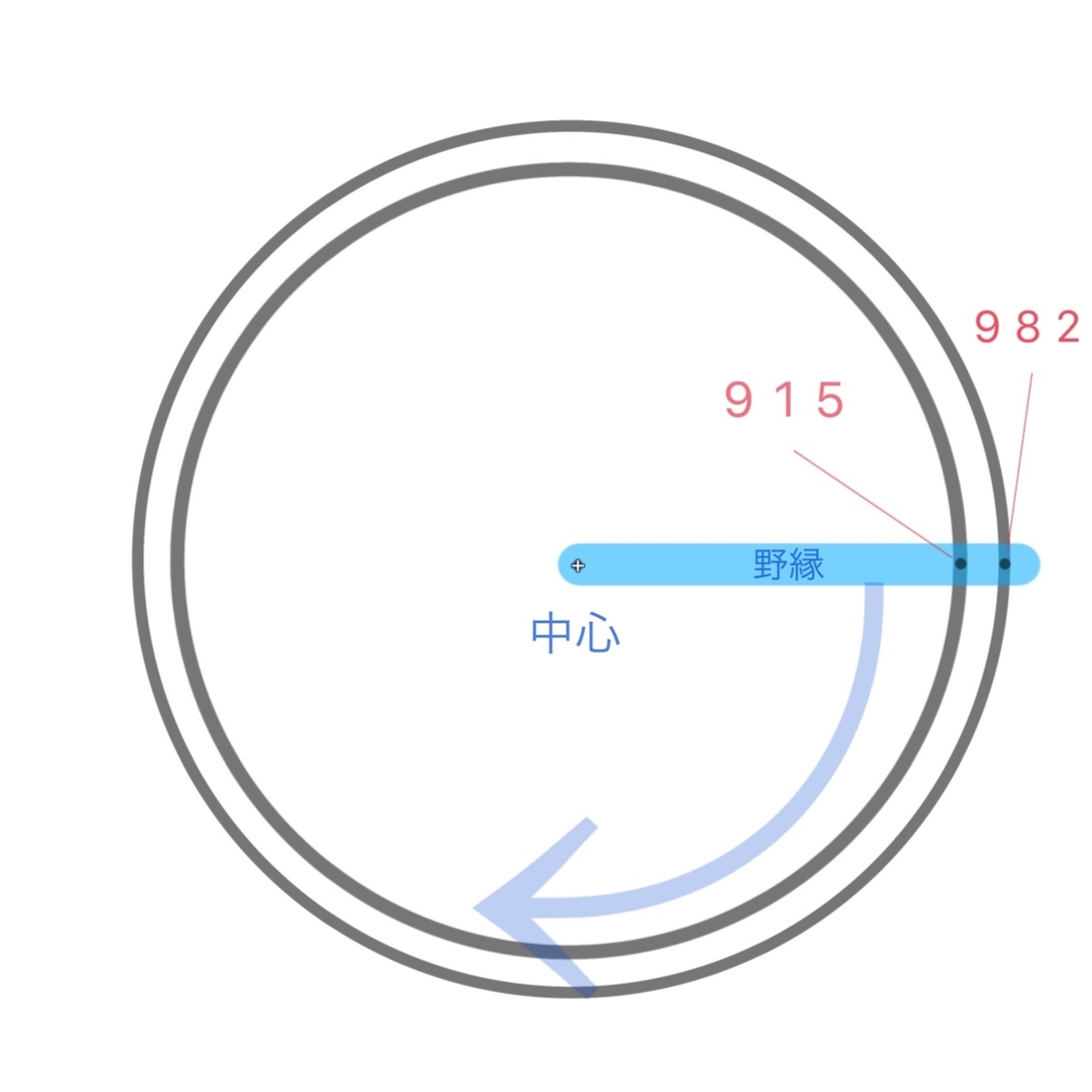
この場合は単純に野縁などの軽鉄材に982mm間隔の穴を空けて、中心となる位置からコンパスのように描くことが一番簡易的な方法として考えられます。
これでLGSの外側で墨出しができるので、65型のランナーを使用して壁を立てる場合は982mmからさらにランナーの幅分67mm引いた915mmで内側の墨出しもできます。
また、単純に 下図のようにレーザー墨出し器を使用して中心から十字に墨を出して、出した墨の端を繋いでいき、その中点と中心を繋ぐことを繰り返し行う方法もあります。
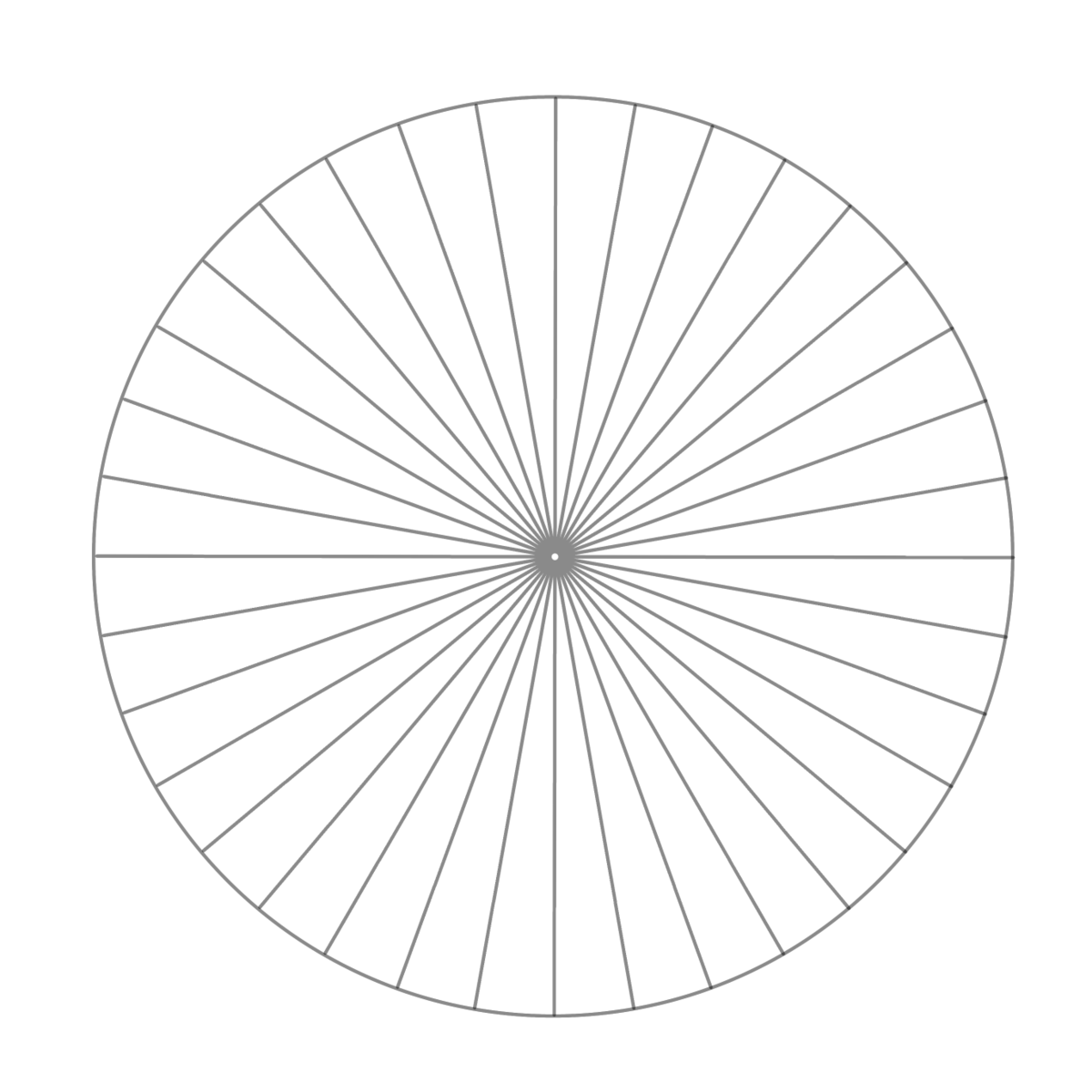
中心からRの長さで、4〜8〜16〜32〜64と多方向にRの長さで墨を出す方法もあります。
大きなRの墨出し
小さなRの墨出しは物を使ってコンパスで描くように墨を出せたかと思いますが、今度は大き過ぎて小細工は通用しないくらいのRの場合はどうすれば良いのか解説していきます。
円は分割して直線の墨をいくつも出す
Rは大きくなればなるほどカーブが緩くなり大きさにもよりますが、分割した一部分だけで見ると直線とほぼ変わらないくらいになります。
下図のように 小さいほど細かく、大きいほど広く、円を分割して墨を出します。

では、どのようにして円を分割して その位置を求めていくかが難関なわけです。
円の位置の求め方
円が描かれる時にRの通る位置がわかれば、それを線で繋いで円に 近づけていくことができます。
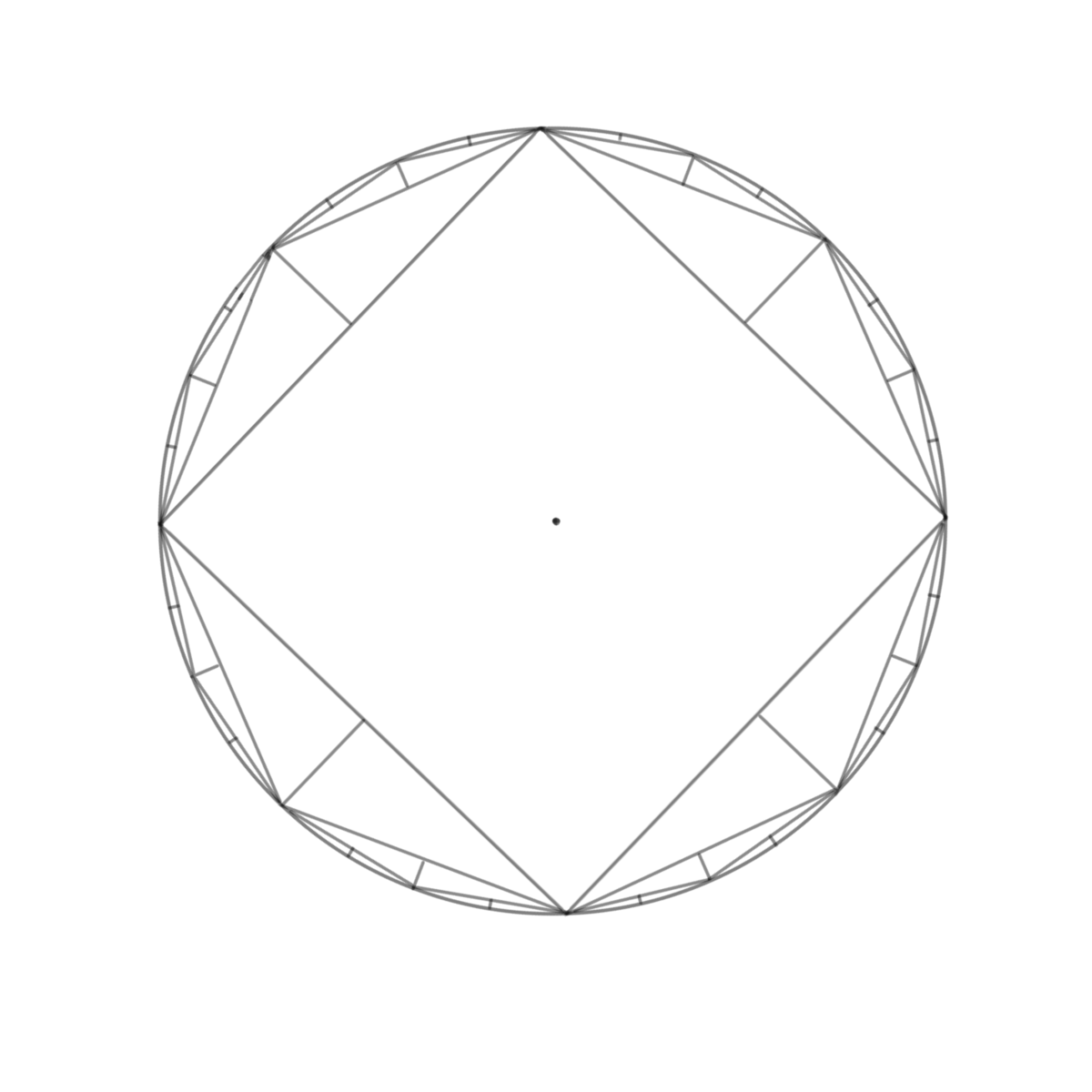
必要な情報は円を作るなら中心の点の位置と半径です。
まず、円の元となる正四角形を作ります。

XとYの逃げ墨(返り墨、寄り墨)と中心点とRから上図の赤線を出します。
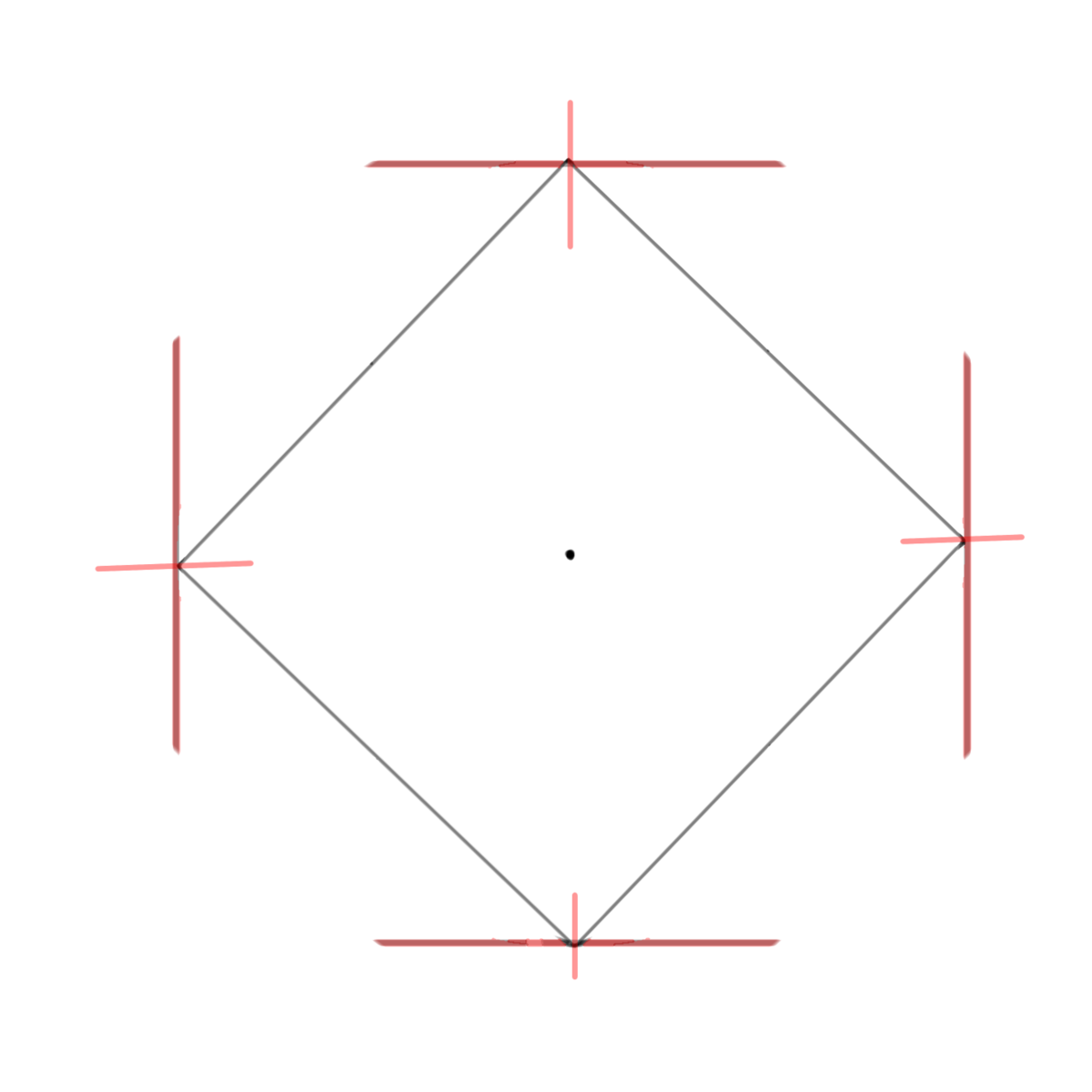
直径の端を繋ぐと四角になります。
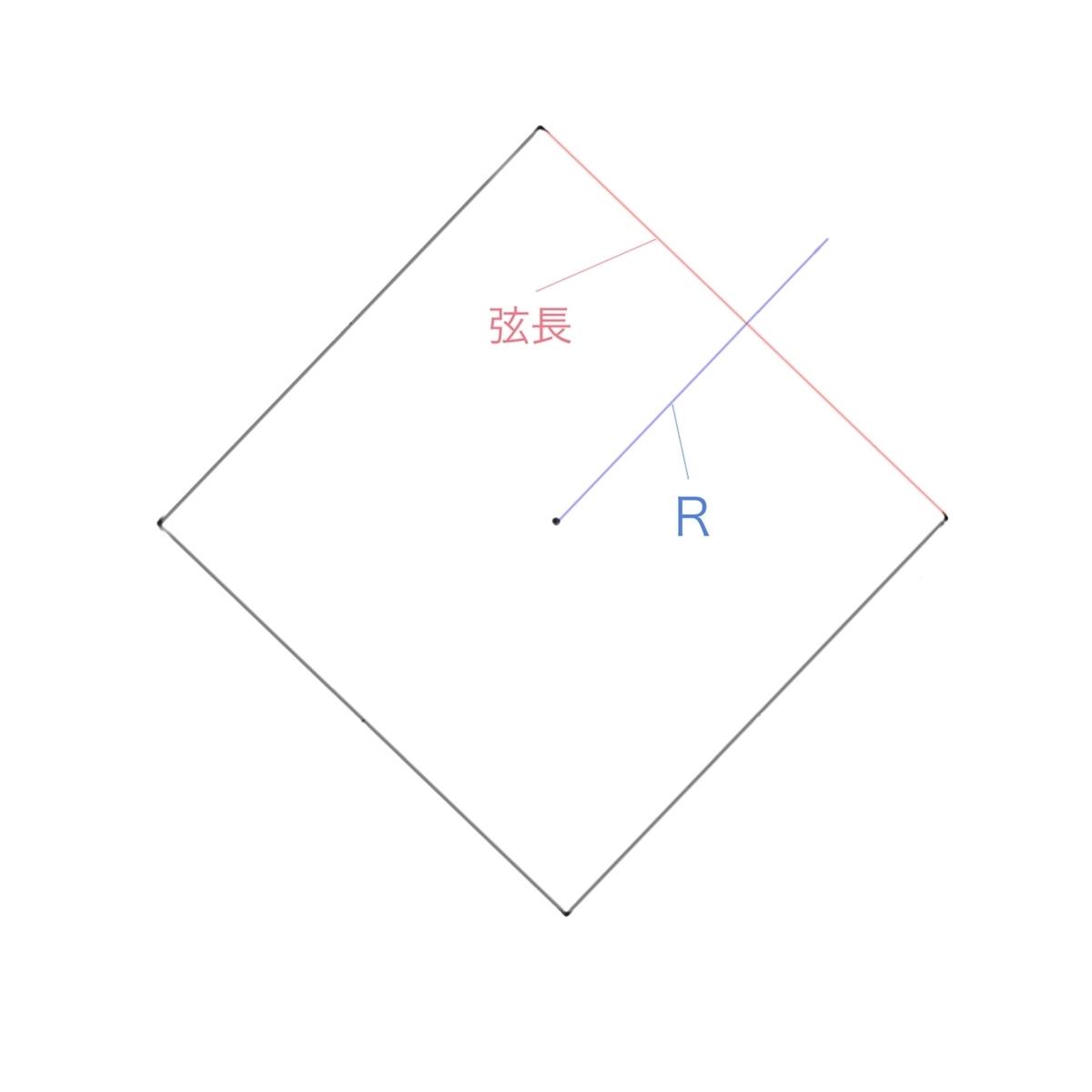
この段階で、Rの数値と上図の赤線部分の弦の長さがわかるので それらの数値を利用して計算していきます。
簡易的な計算ではまともな近似値(ここでは綺麗な円に近い、より正確な数値のこと)を求めることができませんので、難しい計算をしますが 公式を暗記したり計算機に入力したりと手間がかかったり間違えたりする可能性が出てきます。
難しい公式とニュートン・ラフソン法で計算すると欲しい数値が出てくるらしいのですが、無理です。わかりません。笑
ですので、頭の良い人が作ってくれた下記計算サイトを利用して数値を求めていきます。
上記計算サイトで現状わかっている数値を入力して不明な値は0と入力します。
半径(R)と弦長がわかるので、2つの値を埋めると残りの値を計算して出してくれます。
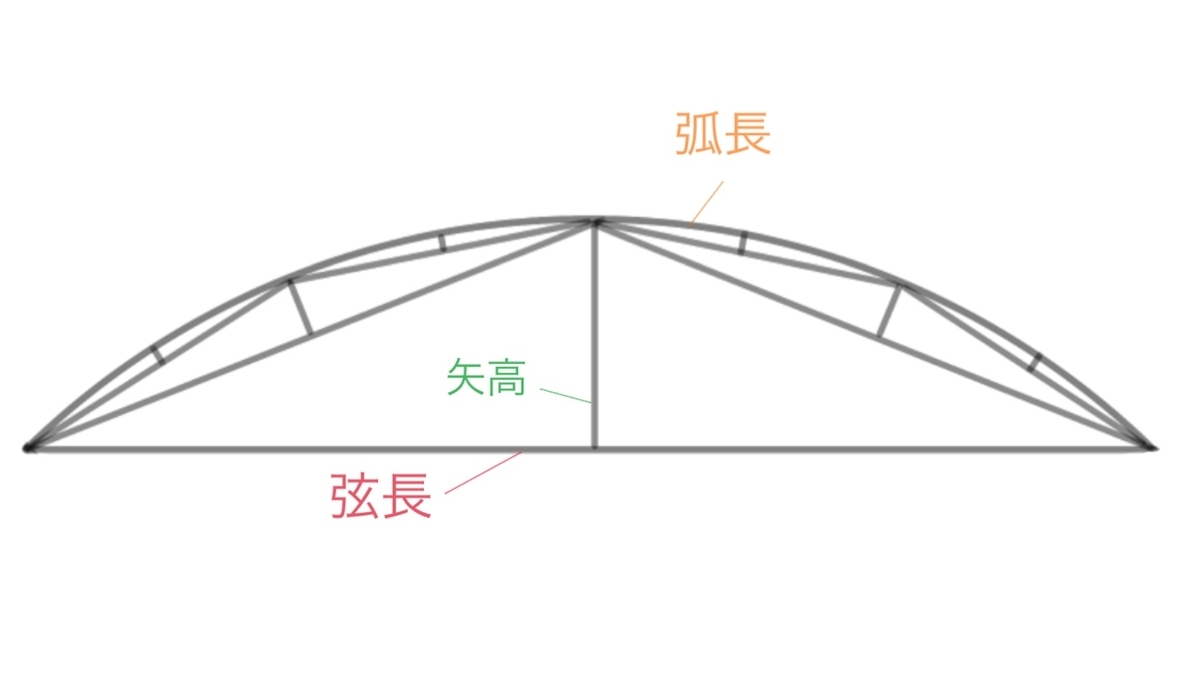
円を分割した一部分のことを円弧(えんこ)と言いいます。これを4方向繰り返して墨をだしていきます。
先ほどの上記の計算を行うと矢高と弧長がわかります。
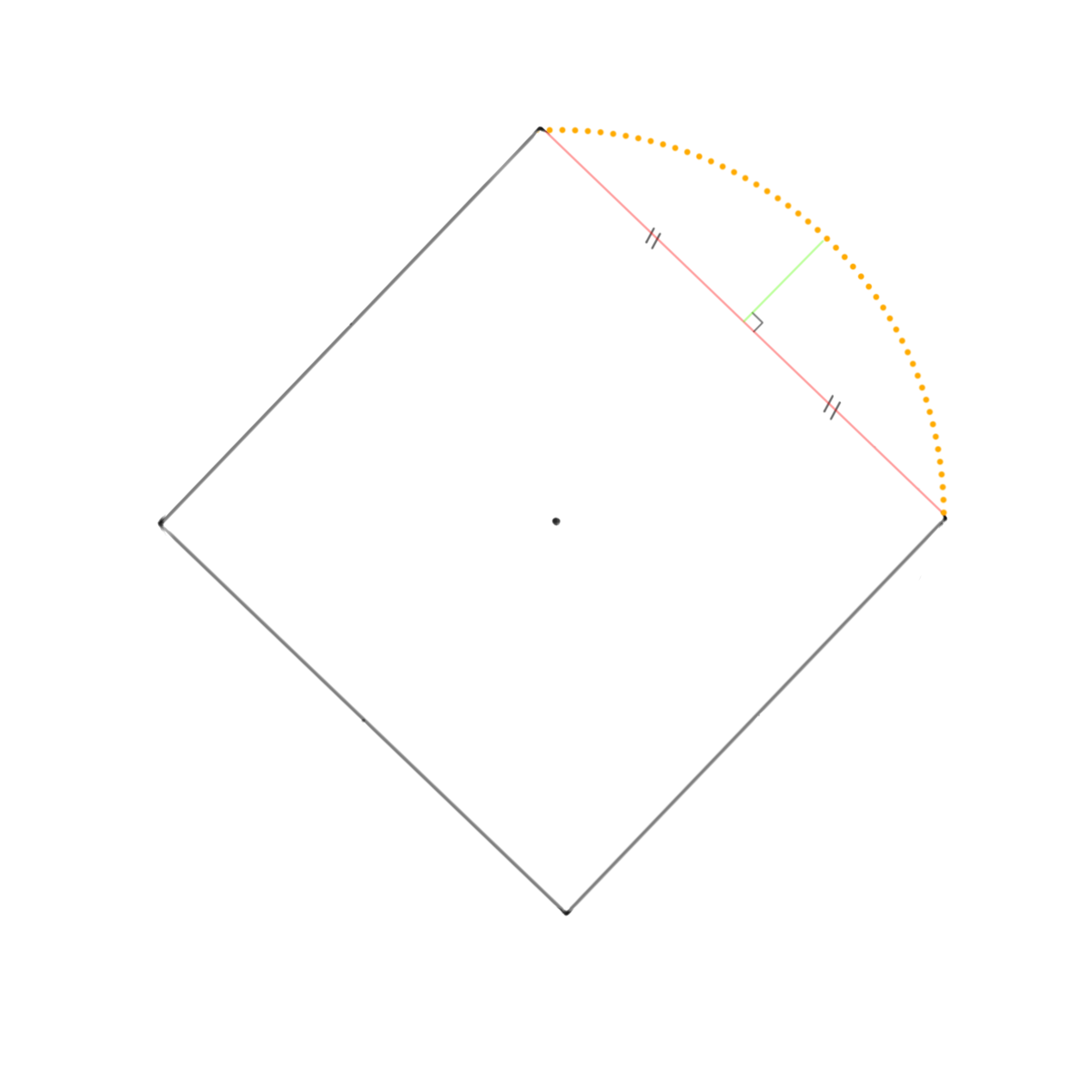
上図のように、弦長を二等分した位置から レーザー墨出し器を利用して直角に矢高の墨を出します。
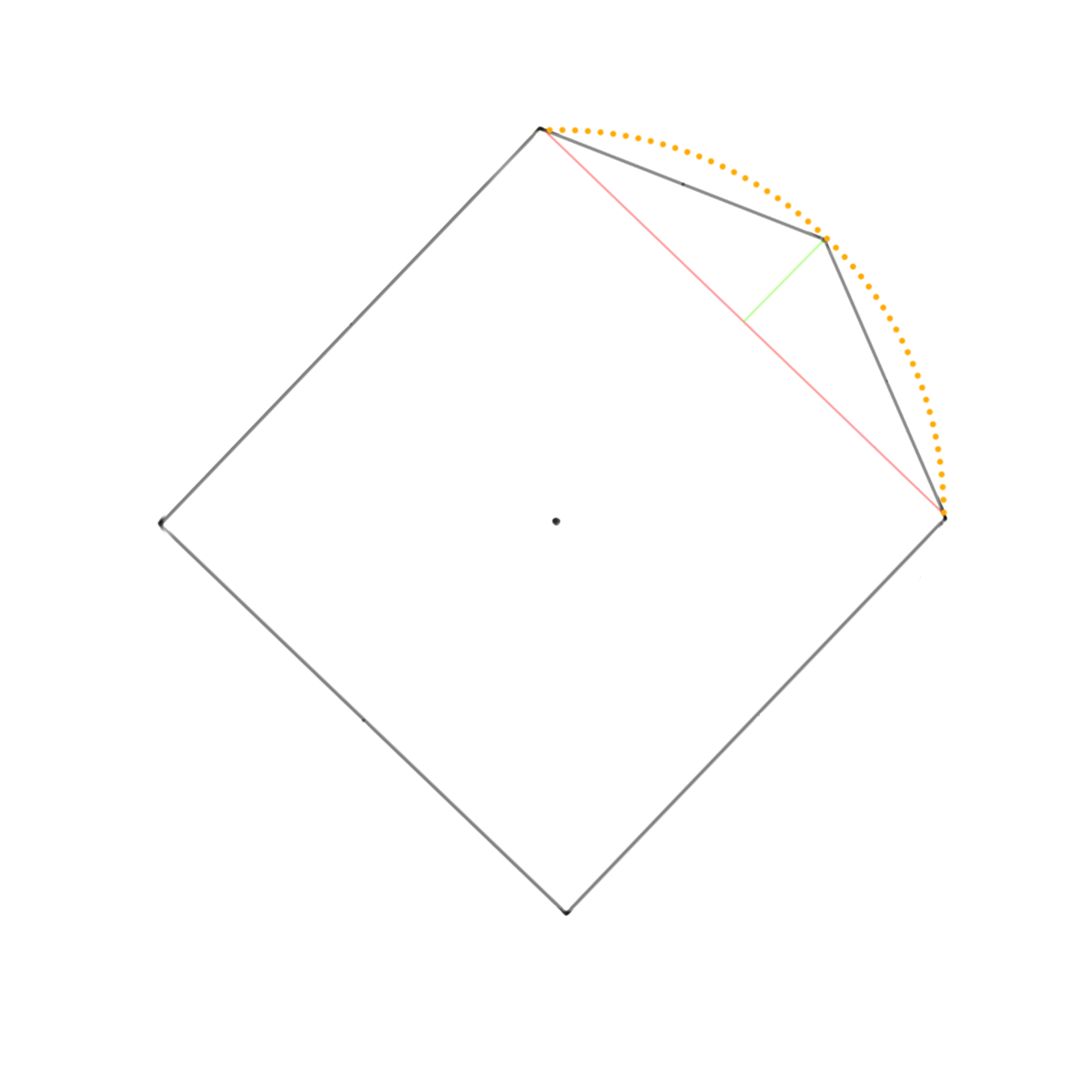
出した矢高を頂点として四角の頂点2箇所と墨で結びます。
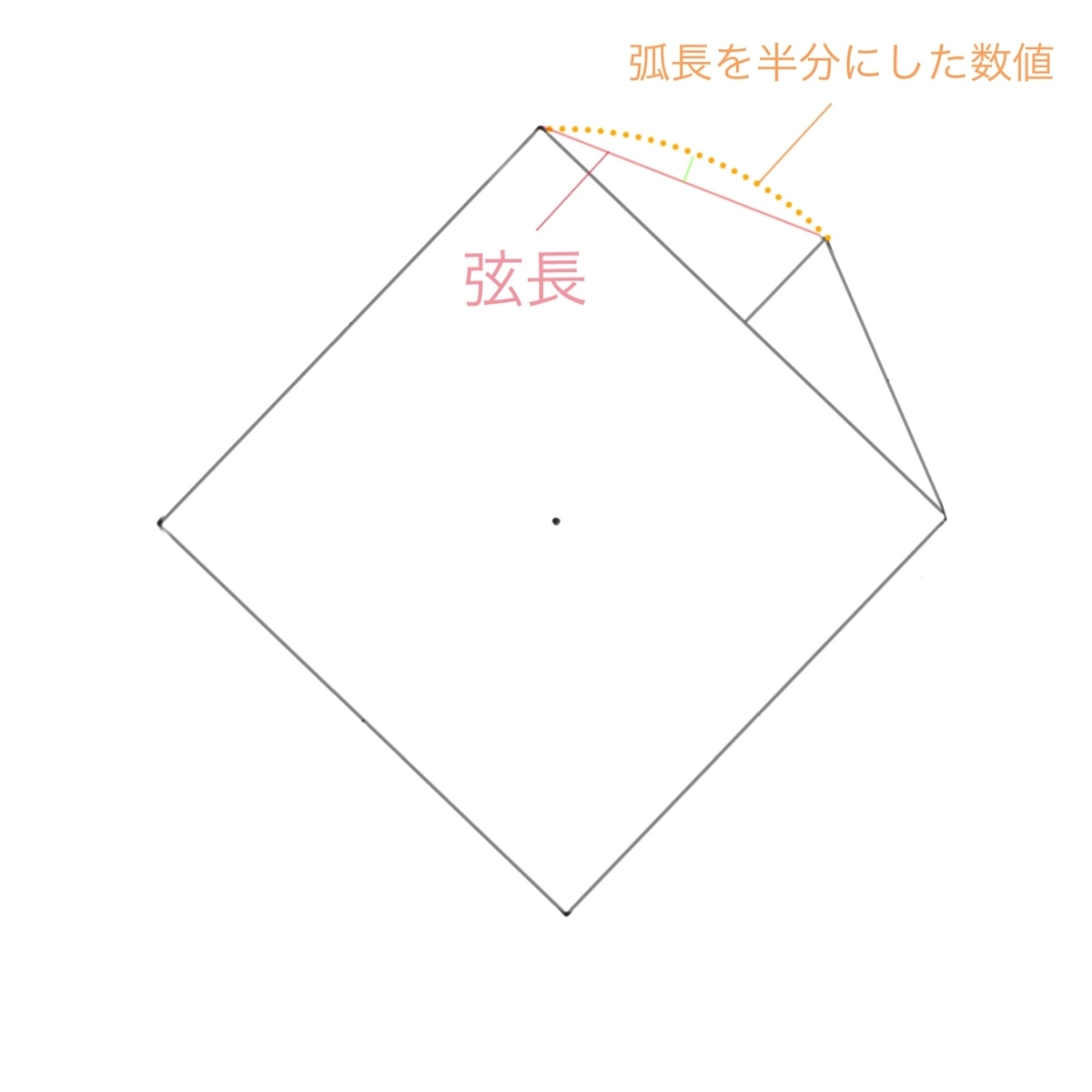
次に初めの計算で求めた弧長を半分にした数値と上図の赤線を弦長として計算して矢高を求めます。
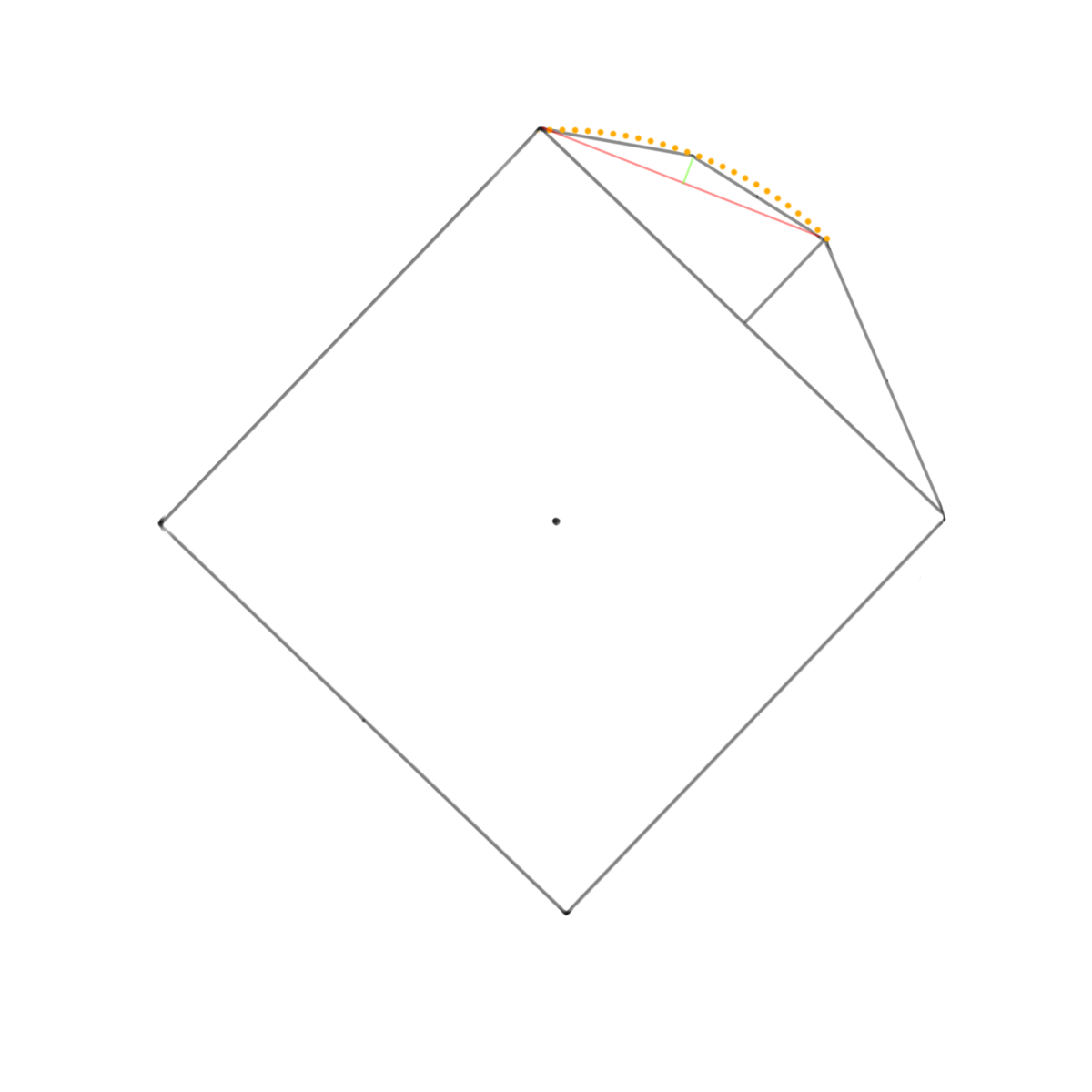
先ほど同様に矢高を頂点として弦の両端と墨で結びます。
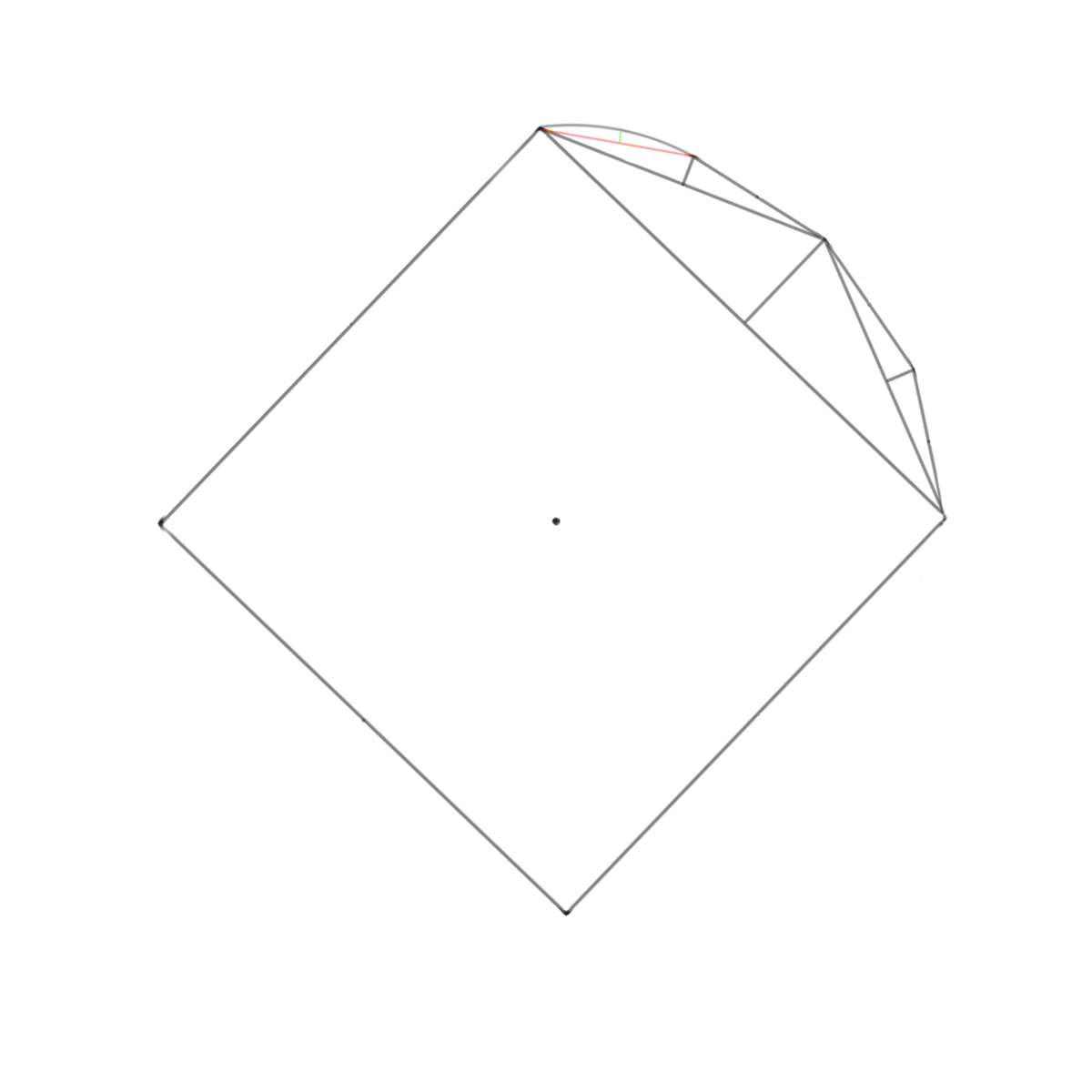
初めの計算で求めた弧長から4分の1にして先ほどと同じように計算していきます。
こうして繰り返していくと下図のように墨出しを行うことができます。
もっと細かく分割したい場合はさらに8分の1、16分の1、32分の1と計算していきます。
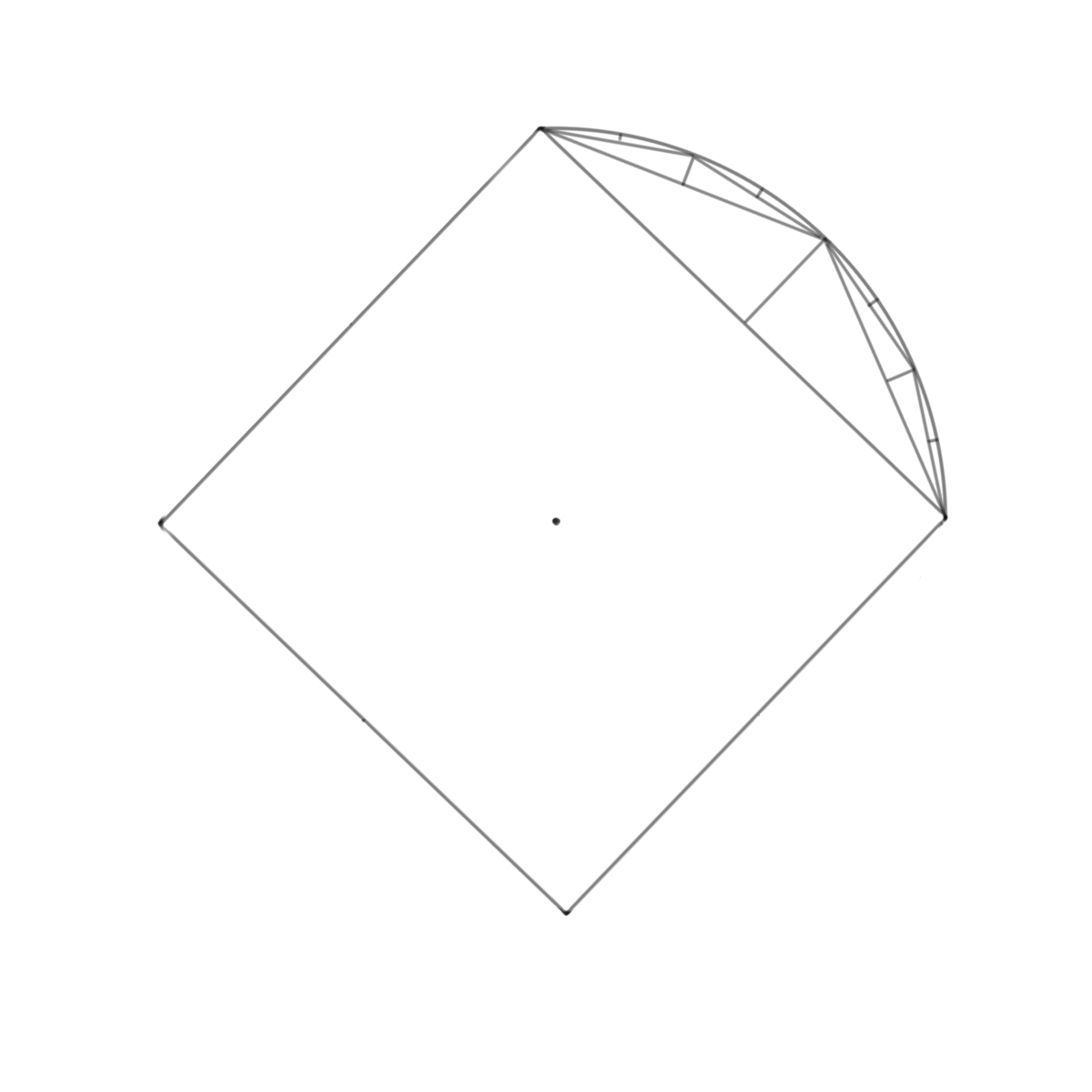
これを四方繰り返し
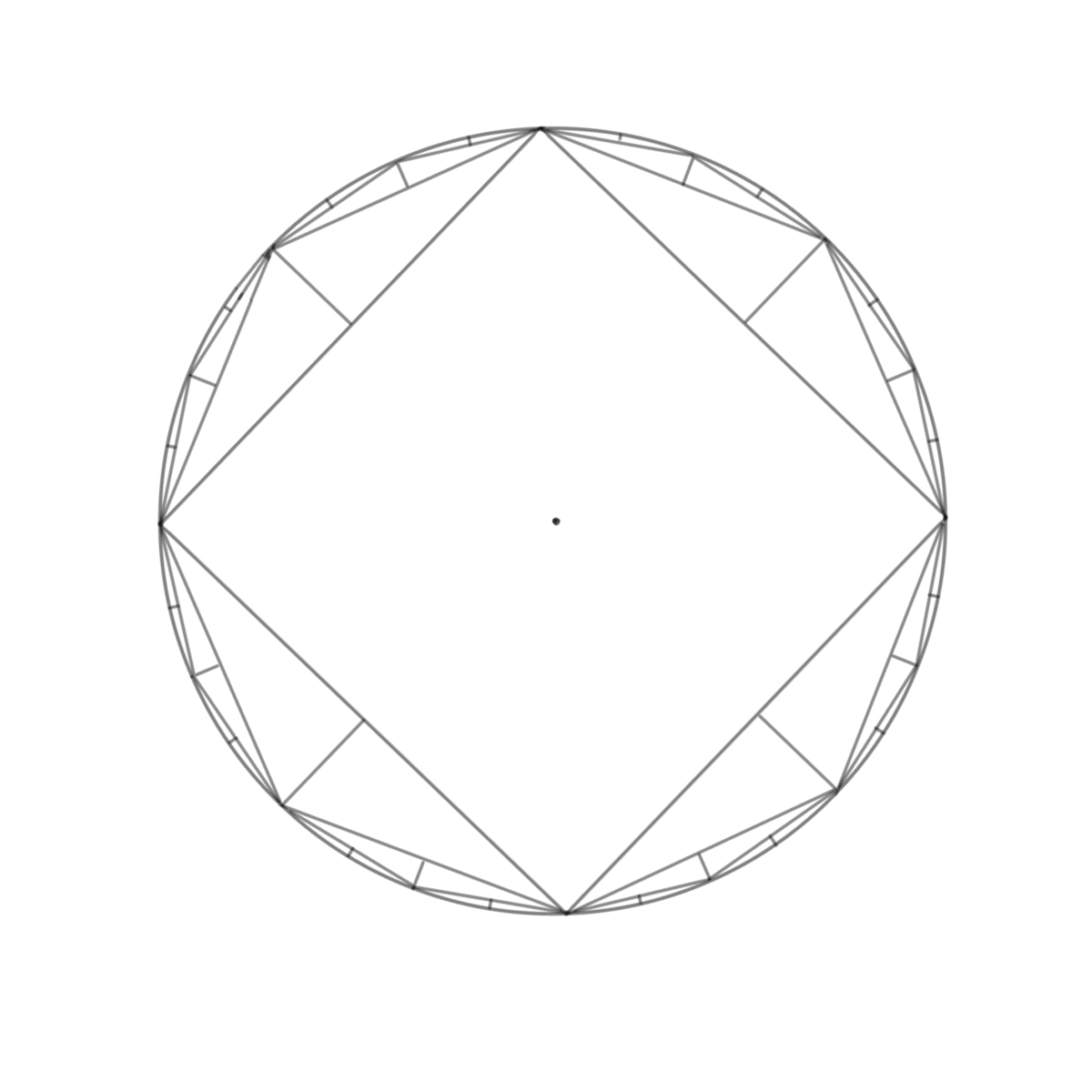
こうして円の墨出しが完了します。
上記サイトの計算でできそうにもない場合、例えば弦長の位置に障害物があって途切れてしまう時は 円弧高さ 円弧長さ 円弧長さ 円弧幅の計算 (1)や円弧高さ 円弧長さ 円弧長さ 円弧幅の計算 (2)も駆使しながら状況に応じて 当てはめて計算していくと上手く墨を出せるかと思います。